Principale différence: dans les ordinateurs, les arbres binaires sont des structures de données arborescentes qui stockent les données et permettent à l'utilisateur d'accéder aux données, de les rechercher, de les insérer et de les supprimer au moment de l'algorithme. La différence entre un arbre B et un arbre B + réside dans le fait que, dans un arbre B, les clés et les données peuvent être stockées à la fois dans les nœuds internes et terminaux, tandis que dans un arbre B +, les données et les clés ne peuvent être stockées que dans les nœuds terminaux. .
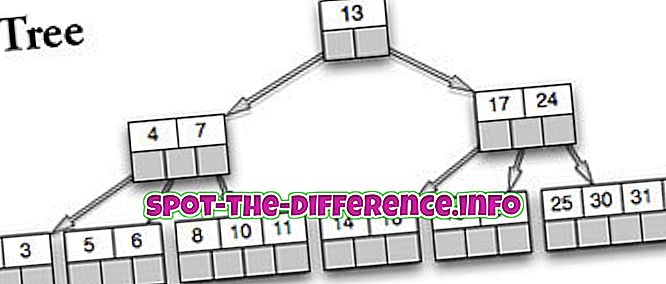
Les arbres binaires sont des arbres de recherche équilibrés conçus pour fonctionner correctement sur les périphériques de stockage secondaires à accès direct tels que les disques magnétiques. Rudolf Bayer et Ed McCreight ont inventé le concept d’un arbre à branches.
Un arbre B est un arbre de recherche binaire généralisé, dans lequel tout nœud peut avoir plus de deux enfants. Chaque nœud interne dans un arbre B contient un certain nombre de clés. Ces clés séparent les valeurs et forment ensuite les sous-arbres. Les nœuds internes d'un arbre B peuvent avoir un nombre variable de nœuds enfants, disposés dans une plage prédéfinie. Au moment où des données sont insérées ou supprimées d'un nœud respectif, le nombre de nœuds enfants change. Afin de maintenir la plage prédéfinie, les nœuds internes peuvent être joints ou divisés. Dans un arbre B, une plage de nœuds enfants est autorisée, en conséquence de quoi la plage prédéfinie doit être conservée.
Les arbres B ne doivent pas être rééquilibrés fréquemment, contrairement aux autres arbres de recherche à auto-équilibrage. Les nœuds dans ces arbres ne sont pas toujours pleins; par conséquent, les espaces sont consommés de manière inutile dans ces arbres, ce qui entraîne un gaspillage d'espace. Seules les limites inférieure et supérieure du nombre de nœuds enfants sont généralement fixées pour une implémentation particulière. Par exemple, dans une arborescence 2-3 B-tree (souvent simplement appelée une arborescence 2-3), chaque nœud interne peut avoir uniquement 2 ou 3 nœuds enfants.
De plus, le B-tree est optimisé pour les systèmes qui lisent et écrivent des blocs de données volumineux. Il est couramment utilisé dans les bases de données et les systèmes de fichiers. Dans l'arborescence B, tous les nœuds sont conservés aux mêmes profondeurs d'équilibrage à partir des nœuds racine. Ces profondeurs augmentent lentement à mesure que le nombre d'éléments augmente; il en résulte que tous les nœuds terminaux sont un nœud supplémentaire, plus éloigné de la racine. En outre, les arbres B- sont plus avantageux que d'autres implémentations en ce qui concerne le temps nécessaire pour accéder aux données.

Une arborescence B + est une arborescence de tableaux multiples avec un nœud, composé d'un grand nombre d'enfants par nœud. La racine peut être une feuille ou un nœud contenant plus de deux enfants. Un arbre B + comprend une racine, des noeuds internes et des feuilles.
Un arbre B + est identique à un arbre B; la seule différence est que, dans l'arbre B +, un niveau supplémentaire est ajouté au bas avec des feuilles liées. De même, contrairement à l’arborescence B, chaque nœud d’une arborescence B + ne contient que des clés et non des paires clé-valeur.
De plus, le facteur d'équilibrage ou l'ordre d'un arbre B + mesure la capacité des noeuds internes d'un arbre, c'est-à-dire le nombre de noeuds qu'ils peuvent avoir. Le nombre réel d'enfants pour un nœud est limité pour les nœuds internes. La racine est toutefois une exception car il est autorisé d'avoir plus de deux enfants. Par exemple, si l'ordre d'un arbre B + est 7, chaque nœud interne (à l'exception de la racine) peut avoir entre 4 et 7 enfants; alors que la racine peut avoir entre 2 et 7. La principale valeur de l’arborescence B + réside dans le stockage des données pour une extraction efficace dans un contexte de stockage orienté par blocs et dans des systèmes de fichiers particuliers.
La valeur principale de l’arbre B + réside dans le stockage et la maintenance des données, afin que celles-ci ne soient pas perdues. Cette approche est particulièrement appliquée dans le contexte de stockage orienté par blocs et dans certains systèmes de fichiers. Les feuilles, qui sont les blocs d'index les plus bas, de l'arbre B + sont souvent liées les unes aux autres dans une liste chaînée; par conséquent, cela rend les requêtes de plage ou une itération ordonnée à travers les blocs plus simples et plus efficaces. De plus, le facteur d'espace n'est pas perdu dans les arbres B +. L'arborescence B + fournit un format de structure de données de logement efficace, ce qui facilite leur accès et leur stockage. Les arbres B + sont particulièrement utiles en tant qu'index système de base de données, où les données résident généralement sur un disque.
Comparaison entre B Tree et B + Tree:
Arbre B | Arbre B + | |
Descriptions web courtes | L’arborescence AB est une structure organisationnelle permettant le stockage et la récupération d’informations sous la forme d’une arborescence dans laquelle tous les nœuds terminaux sont à la même distance de la base et tous les nœuds non terminaux ont entre n et 2 n sous-arborescences ou pointeurs (où n est un entier). | L'arbre B + est un arbre à n tableaux avec un nombre variable mais souvent élevé d'enfants par nœud. Un arbre B + comprend une racine, des noeuds internes et des feuilles. La racine peut être une feuille ou un nœud avec deux enfants ou plus. |
Aussi connu sous le nom | Arbre équilibré. | B plus arbre. |
Espace | Sur) | Sur) |
Chercher | O (log n) | O (log b n) |
Insérer | O (log n) | O (log b n) |
Effacer | O (log n) | O (log b n) |
Espace de rangement | Dans une arborescence B, recherchez des clés et des données stockées dans des nœuds internes ou terminaux. | Dans un arbre B +, les données stockées uniquement dans des nœuds terminaux. |
Les données | Les noeuds feuille des trois magasins pointent sur des enregistrements plutôt que sur des enregistrements réels. | Les nœuds d'extrémité de l'arborescence stockent l'enregistrement réel plutôt que des pointeurs vers des enregistrements. |
Espace | Ces arbres gaspillent de l'espace | Là les arbres ne perdent pas de place. |
Fonction des nœuds feuilles | Dans l'arborescence B, le nœud feuille ne peut pas stocker à l'aide d'une liste liée. | Dans l'arborescence B +, les données du nœud feuille sont classées dans une liste chaînée séquentielle. |
Recherche | Ici, la recherche devient difficile dans B-tree car les données ne peuvent pas être trouvées dans le nœud feuille. | Ici, la recherche de toutes les données dans une arborescence B + est très facile car toutes les données se trouvent dans des nœuds feuilles. |
Recherche d'accessibilité | Ici, dans l’arbre B, la recherche n’est pas aussi simple que celle d’un arbre B +. | Ici, dans l'arborescence B +, la recherche devient facile. |
Clé redondante | Ils ne stockent pas de clé de recherche redondante. | Ils stockent la clé de recherche redondante. |
Applications | Ils sont une version plus ancienne et ne sont pas si avantageux par rapport aux arbres B +. | De nombreux développeurs de systèmes de base de données préfèrent la simplicité structurelle d'un arbre B +. |