Différence essentielle: une parabole est une section conique créée lorsqu'un plan coupe une surface conique parallèle au côté du cône. Une hyperbole est créée lorsqu'un plan coupe une surface conique parallèle à l'axe.

Parabole et hyperbole sont deux mots, sections et équations différents utilisés en mathématiques pour décrire deux sections différentes d'un cône. Celles-ci diffèrent par leur forme, leur taille et divers autres facteurs, y compris les formules utilisées pour le calculer. Pour les comprendre, commençons par comprendre le cône et les différentes sections coniques.

Une section conique est une courbe obtenue lorsqu'un plan coupe un cône de différentes manières. Les coupes obtenues à partir de l'intersection incluent l'ellipse, le cercle, la parabole et l'hyperbole. Selon la géométrie analytique, conique est défini comme «une courbe algébrique plane de degré 2.» La définition courante de la section conique inclut un point de focalisation, une droite directrice et une excentricité. Le point de focalisation et les lignes de la directrice doivent être dans une ration fixe dans une conique. Le rapport est connu comme l'excentricité de la section conique. L'excentricité des ellipses, des paraboles et des hyperboles diffère; les ellipses ont une excentricité inférieure à 1, les paraboles ont une excentricité égale à 1 et les hyperboles ont une excentricité supérieure à 1. Le plus ancien travail connu sur les sections coniques peut être daté du IVe siècle av. J.-C. par Menaechmus, qui a découvert pour résoudre le problème de doubler le cube par l'utilisation de paraboles.

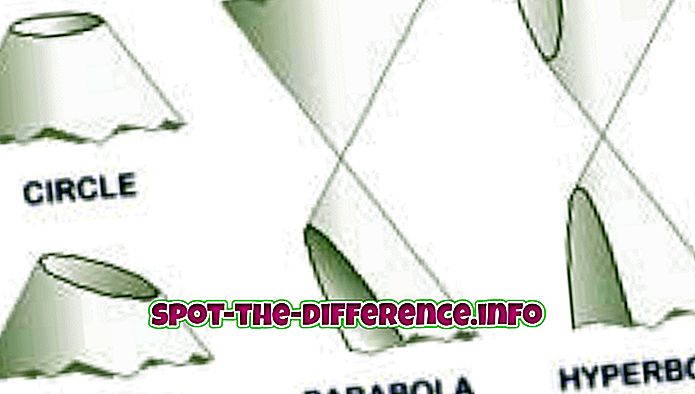
Une parabole est une section conique créée lorsqu'un plan coupe un cône. Des paraboles ou des paraboles se forment «à l’intersection d’une surface conique circulaire droite et d’un plan parallèle à une droite génératrice de cette surface». Une parabole est également créée lorsqu'un locus de points sur un plan équidistants du focus et de la directrice crée une parabole. En algèbre, les paraboles sont couramment utilisées dans les graphes de fonctions quadratiques, en utilisant la formule y = x ^ 2.

Une ligne qui sépare la parabole en son milieu est appelée axe de symétrie. cette ligne est également perpendiculaire à la directrice et traverse le foyer. Les points situés sur l'axe de symétrie qui intersectent la parabole sont appelés «sommets». La distance entre le sommet et le foyer est appelée "distance focale". Les paraboles peuvent s'ouvrir dans les deux sens: haut, bas, droite ou gauche. Une des caractéristiques principales des paraboles est qu’elles sont toutes identiques et ne diffèrent que par leur taille. Ils peuvent être repositionnés et redimensionnés pour s’adapter parfaitement à toute autre parabole. Les paraboles sont utilisées dans diverses applications telles que les réflecteurs de phares d'automobiles, la conception de missiles balistiques, etc. Elles jouent également un rôle majeur en physique, en ingénierie, en mathématiques, etc.

Les hyperboles sont une courbe lisse qui se produit lorsqu'un plan coupe le cône parallèlement à l'axe des ordonnées, ce qui crée une coupe le long du cône. Une hyperbole est définie par ses propriétés géométriques ou ses équations pour lesquelles elle constitue un ensemble de solutions. Le terme «hyperbole» est dérivé du mot grec qui signifie «renversé» ou «excessif». On pense que ce terme a été inventé par Apollonius de Perga, qui a grandement contribué à l’étude des sections coniques.

On sait qu'une hyperbole a des branches qui sont des images inversées et qui ressemblent à deux arcs infinis. Les points des deux branches les plus proches s'appellent les sommets. La ligne qui relie les sommets est appelée axe transversal ou axe principal, ce qui correspond au diamètre principal d'une ellipse. Le centre de l'axe transversal est appelé centre de l'hyperbole. L'équation d'une hyperbole est écrite sous la forme x2 / a2-y2 / b2 = 1. Les hyperboles sont utilisées dans diverses applications du monde actuel, notamment le trajet suivi par l'ombre de la pointe d'un cadran solaire, la forme d'une orbite ouverte; il est utilisé comme arche dans de nombreux bâtiments construits, comme équations en mathématiques et géométrie, en physique, etc.

Les hyperboles et les paraboles sont toutes deux des courbes ouvertes, ce qui signifie qu'elles ne se terminent pas et continuent indéfiniment à l'infini, ce que les ellipses et les cercles ne peuvent pas faire.